This financial calculator determines the underlying interest rate of an installment loan. This is the rate that is consistent with initial balance, final balance and installments of a loan contract. The calculator works for loan types with fixed interest and constant installments, such as mortgages, car loans and consumer credits. Usage instructions and explanations on the economics of installment loans follow after the calculation form.
Usage Instructions for Loan Interest Rate Calculator
Please fill the calculator form with the amount of the loan paid out to you, the outstanding loan amount at end of term, the height of regular installments, and the term of the loan in years. All fields above the calculate button are input values, which you can change as needed. From these inputs the form will calculate the loan interest rate.
The term of the loan is same as the contract duration, or the number of years you will have to pay off the loan.
Per default, the form sets twelve annual installments equivalent to monthly payments in its number of installments input field. Since mortgages or car loans usually require monthly payback, most users will be fine with this setting. However, you may override this to four (quarterly payments), two (semi-annual payments) or one (annual payments).
In addition to the loan interest rate, the calculator outputs intermediate balances in the details section. Since this list can grow quite long, you may choose to hide it clicking the “hide -” label in its upper right corner.
How Installments Affect the Loan Interest Rate
This section explains the dependency between the height of installments and underlying interest rate. Generally, with initial and ending loan balances as well as the contract duration fixed, the underlying interest rate rises with the height of installments.
For each combination of loan balances and installment amounts, there is up to one underlying interest rate that brings the values into line. So if the selected conditions make sense and fit a loan agreement, the calculator can find a solution. Otherwise it issues the message “Error in computation loop”. An example of such a value combination that cannot result in a meaningful loan agreement would be a positive loan amount, which is to be fully repaid with negative installments.
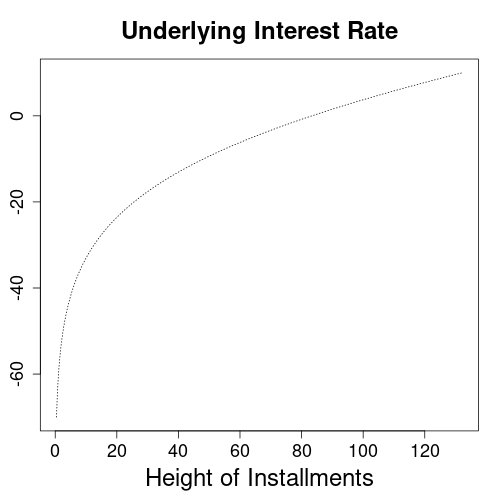
See the above graph as an example for unrealistic lending scenarios, that can still make sense as loan agreements. The graph has interest rates on its vertical axis and monthly installments on its horizontal axis. So the dotted line plots underlying interest rates for various heights of monthly installments. All scenarios assume a $10,000 loan to fully repay over a time-span of 10 years. For instance, if we could find a lender charging -70% of interest, then less than $1 per month would suffice to clear the loan. That’s because with negative interest, the lender will be paying the borrower for taking his money.
If however we take realistic lending scenarios, such as a monthly installment of $110, then the calculator will come up with reasonable interest rates of around 5.8%.
Mathematical Formula
The calculator form uses the following formula to calculate underlying interest rates for loans:
I(r) = r / m / ((1 + r/m)(m*t) - 1)
* (L0 * (1 + r/m)(m*t) - L1)
argminr { Inst - I(r) }
Inst: installment amount
I(r): installment amount as function of interest rate r
r: interest rate
m: number of installments per year
t: duration of loan contract in years
L0: loan amount paid out at start
L1: remaining loan balance at end of contractBecause the interest rate r enters the formulas for installment loans in several powers, there is no straightforward analytical solution. However, we can reuse the formula for the installment given an interest rate and loan amounts. The calculator will then be looking for an interest rate r for which the height of installment formula outputs a value close to a desired target. This is expressed in the argminr. It says that the calculation loop is trying candidate values for the interest rate r to minimize the difference between target installment Inst and I(r).
With a suitable solver algorithm, the computation finds high precision solutions in less than 10 iterations.
References
Amortization calculator: Wikipedia.org
Similar Computations
Height of Installment for Installment Loans: finalgebra.com
Underlying Interest Rate for Installment Loans in German: zinseszins.de